| Table 1. Paternity inference based on counting inconsistencies | |||
|---|---|---|---|
| inconsistencies | rate among false trios | rate among true trios | LR supporting paternity |
| 0 | 1/210 000 | 0.97 | 200 000 |
| 1 | 1/10 000 | 1/35 | 290 |
| 2 | 1/1100 | 1/2600 | 1/2.4 |
| 3 | 1/190 | 1/320 000 | 1/1700 |
| 4 | 1/48 | 1/61 000 000 | 1/1 300 000 |
The mutation inconsistency rate for true trios at STR loci
appears to average about 1/400
[AABB, Brinkmann, Kayser,
unpublished data]. Assuming a 13 marker paternity test
and binomial model, the expectations are shown in Table 1
[corrected August 2010 — thanks to Giuseppe Cardillo, Naples.]
Clearly, two inconsistencies is the critical case. Prima facie it supports non-paternity by a likelihood ratio of 2.4, which is inconclusive. This paper examines more closely the case of two inconsistencies.
Mutations are generated according to a modified stepwise mutation model, which assumes that most mutations are by plus or minus one repeat unit and are paternal.
The model parameters [5, 6] are:
- μ = rate of one-step paternal mutations (locus-dependent)
- i = proportion of mutations that increase size. i=½ for this study.
- rs = factor by which |s+1| step mutations are rarer than |s| step mutations. (r=20±)
- ma = factor by which maternal mutations are rarer than paternal ones. (ma=3.5±)
Next, a likelihood ratio was computed for each of the 400 cases using the above model.
Covert mutations | |
|---|---|
| common case | another possibility |
| 
|
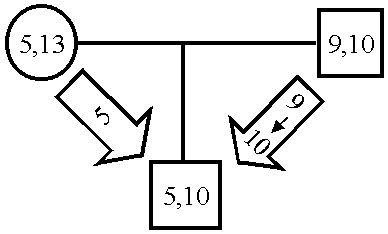
- Covert mutations Analyzing the results of the true-trio simulations revealed an obvious – in retrospect – phenomenon, which we might call "covert mutations" whose significance, so far as I know, has not been previously noted.
- The man contributes the paternal (9) allele by passing not his 9, but
a mutated copy of his 10.
2/3 of covert mutations are of this pattern.
- From child (and mother if present) the paternal allele is ambiguous (9 or 13);
the man matches one of them (9) but through mutation it is the other one (13)
that he contributes.
1/3 of covert mutations are of this pattern.
- Two inconsistencies
As table 1 shows, if one merely counts inconsistencies without regard to the particulars, a finding of two inconsistencies is modest evidence favoring non-paternity. Table 2 shows that taking into account the rarity of shared alleles and the plausibility as mutations of inconsistencies – i.e. computing the paternity index (PI) – somewhat distinguishes true from false trios.
The figures illustrates ways that a mutation may go unnoticed.
| Table 2. Distribution of PI's among simulated 2-inconsistency cases | ||
|---|---|---|
| x | % false trios with PI>x | % true trios with PI>x |
| 1000 | 0% | 4.5% |
| 100 | 0 | 19 |
| 10 | 0.5 | 43 |
| 1 | 3 | 78 |
| 1/10 | 20 | 95.5 |
| 1/100 | 47 | 99.5 |
- Covert mutations The significance of covert mutations is that since all published estimates of mutation rates are derived from paternity studies, all of the ones for autosomal loci are too low by a possibly significant amount. The rate of apparent mutations is the right number to use to calculate table 1, but for case calculations – table 2 – the covert-adjusted must be used. For example, in CSF1PO apparent μ=3/1000 but the true μ=4/1000. Failure to account for covert mutations thus inflates paternity indices, so is anti-conservative. There may also be an implication in evolutionary studies when a mutational clock is considered.
- Telling true from false
Considering that true trios predominate over false ones in paternity
laboratories, cases with two inconsistencies are false trios by a
margin of only 2:1. "Paternity excluded" based on two inconsistencies
is a very poor policy. Computing a likelihood ratio is the proper
course. Interpreting it, though, can be a problematic when it is small.
The 19% of true trios with PI>100 notwithstanding the two mutations, can possibly be reported (with so-called "paternity probability" > 99%) and the burden of interpretation left to the judge. A majority of the true trios will have 1/10 < PI < 100 and are obviously inconclusive. Possibly further testing will help; nothing else will.
- What to do?
Once the untenable policy of the past – pretending in effect that PI=0
whenever some target number of inconsistencies are observed – is
abandoned, one is confronted with making a policy based on interpreting
the true PI. For example, if PI=1/10000 reporting "paternity excluded"
may be acceptable (notwithstanding the paradox that in the symmetrically
opposite case that PI=10000, no one would report "paternity certain").
But what of the less extreme cases with a smaller PI, such as 1/10 or 1/100?
Science and justice collide; there is no obvious and acceptable answer.
Assuming, as is customary, a 50% prior probability, the posterior
probability of paternity W is 10% or 1%. It is well established social
policy that the laboratory doesn't claim "definitely paternity" when
W=99%, so how can it be right for the laboratory to claim "excluded
from paternity" when W=1% - or 0.1% for that matter? The
mathematically honest solution of reporting the small PI – whatever it
is after testing resources are exhausted – to a judge who, up to now,
is not prepared for such evidence, is also not very satisfactory.
Fortunately, the situation is infrequent (see table 1). And part of the solution is clear: compute the paternity index correctly, including inconsistent loci. It that is done, it will be seen that occasionally even in some cases with three inconstencies, paternity cannot be excluded. And conversely, there are probably cases that have only one inconsistency but it is of such a nature that it alone effectively rules out paternity.